





| P |
| V |
| T |
| P+dP |
| V+dV |
| T+dT |
| δ W=− |
|
dV |
| δ Q=dU−δ W=mcvdT+nRT |
|
| δ W=−PdV=−nRdT+VdP=−nRdT+nRT |
|
| δ Q=dU+PdV= | ⎛ ⎝ |
mcv+nR | ⎞ ⎠ |
dT−nRT |
|
=mcPdT−nRT |
|
| γ= |
|
= |
|
| CV= |
|
| dU= |
|
| dH= |
|
⎛ ⎝ |
PdV+VdP | ⎞ ⎠ |
| δ Q=dU+PdV= |
|
⎛ ⎝ |
PdV+VdP | ⎞ ⎠ |
+PdV= |
|
| (P,T) | (V,T) | (P,V) | |
| dU | mcvdT | mcvdT | PdV+VdP/γ−1 |
| dH | mcpdT | mcpdT | γ(PdV+VdP)/γ−1 |
| δ W | nRTdP/P−nRdT | −nRTdV/V | −PdV |
| δ Q | mcpdT−nRTdP/P | mcvdT+nRTdV/V | γ PdV+VdP/γ−1 |
| dU= |
|
d | ⎛ ⎝ |
PV | ⎞ ⎠ |
| Δ U= |
|
| δ Q= |
|
=0 |
| γ |
|
+ |
|
=0 |
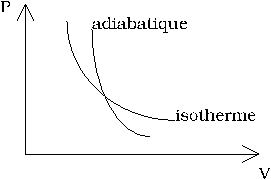
| ⎛ ⎜ ⎜ ⎝ |
|
⎞ ⎟ ⎟ ⎠ |
|
=γ | ⎛ ⎜ ⎜ ⎝ |
|
⎞ ⎟ ⎟ ⎠ |
|
| ⎛ ⎜ ⎜ ⎝ |
|
⎞ ⎟ ⎟ ⎠ |
|
=− |
|
| γ |
|
+ |
|
=0 |
| ⎛ ⎜ ⎜ ⎝ |
|
⎞ ⎟ ⎟ ⎠ |
|
=−γ |
|
| γ= |
|
=1+ |
|


