8 Transferts thermiques
8.1 Introduction.
8.1.1 Flux de chaleur
Les transferts de chaleur jouent un rôle important dans un grand nombre de situations physiques et dans un nombre important d’applications industrielles. Nous allons nous intéresser dans ce cours aux mécanismes du transfert de chaleur plutôt qu’aux relations entre ces transferts de chaleur et les états de la matiére ou avec les autres formes d’énergie. Cet aspect et notamment les relations avec l’énergie mécanique seront examinés dans le cours de thermodynamique qui vous sera dispensé en deuxième année.
Le présent cours se limite donc à l’étude des différents modes de transfert de chaleur. C’est à dire que nous allons examiner comment la chaleur se propage entre deux objets matériels.
Pour commencer, nous devons donner une définition succincte de la notion de chaleur.
Chaleur: Nous appellerons chaleur une quantité d’énergie qui passe d’un corps à un autre sous l’effet d’une différence de température. L’expérience montre en effet que la mise en contact d’un corps chaud ( de température élevée) avec un corps plus froid ( de température plus basse) provoque une évolution au cours de laquelle la température du corps chaud baisse tandis que la température du corps froid augmente. L’interprêtation d’une telle expérience est que le corps chaud a cédé une partie de son énergie au corps froid. C’est ce type d’énergie que nous appellerons chaleur.
Unités: Il résulte de cette définition que les unités de mesure de la chaleur seront les unités d’énergie usuelles. En particulier dans le système S.I., cette unité est le Joule ( Symbole: J ).
Remarque: Il est utile de noter ici la corespondance avec les anciennes unités telle la calorie:
Remarque: On a longtemps considéré que la chaleur était une sorte de fluide (parfois nommé phlogistique) qui s’écoulait entre les corps chauds et froids et par conséquent se conservait. Le développement de la thermodynamique a montré que cette idée était fausse quand d’autre types d’énergies intervenaient en particulier l’énergie mécanique. Ceci a mené à l’idée d’une conservation de l’énergie en général qui correspond mieux à l’expérience. Nous reviendrons sur cet aspect dans le cours de Thermodynamique de deuxième année.
Les énoncés précédents montrent qu’il ne faut pas confondre les notions de chaleur et de température. Bien que dans le langage courant, ces deux mots soient souvent considérés comme équivalents, en physique, il y a lieu de faire une distinction.
La température est un paramètre physique attaché à l’état d’un système. On sait aujourd’hui que la température est une traduction au niveau macroscopique de l’agitation qui a lieu au niveau microscopique (à l’échelle des atomes et des molécules). Plus précisément, la température est une indication du niveau moyen d’énergie cinétique des particules qui constituent la matière. D’un point de vue pratique, on peut classer les différentes températures du plus froid au plus chaud en définissant une échelle de températures. L’échelle de temperature la plus courante est l’échelle Celsius pour laquelle la température est fixée à 0°C pour la glace fondante et à 100°C pour l’eau bouillante sous pression atmosphérique.
Flux de chaleur: On appellera flux de chaleur la quantité de chaleur pasant à travers une surface (ou d’un corps à un autre) par unité de temps. Si l’on note Q la quantité de chaleur déjà passée au temps t, le flux de chaleur peut s’écrire:
Régime permanent: On dira qu’on a atteint un régime permanent lorsque les variables (c’est à dire ici les températures) ne dépendent plus du temps. On dira au contraire qu’on a un régime transitoire lorsque les variables dépendent du temps. Nous nous limiterons ici au régime permanent.
8.1.2 Trois modes de transfert:
On distingue généralement trois modes de transfert de chaleur correspondant à des mécanusmes différents:
Conduction
Le transfert par conduction est un transfert de chaleur par contact matériel. La chaleur se transmet par exemple à travers un solide entre un point chaud et un point froid.
Exemple: Si on trempe dans l’eau bouillante une cuiller en metal, on se brûle en touchant le bout extérieur. La chaleur est passée à travers le métal entre le bout imergé (qui est à une température proche de
) et l’autre bout qui est à une température inférieure. On dit que la chaleur a été conduite par le métal. Les métaux son généralement de bons conducteurs de la chaleur. La même expérience avec une cuiller en bois vous évite de vous brûler car la chaleur passe plus difficilement dans le bois. On dit que le bois est un isolant.
Remarque: On explique ce phénomène par un échange d’énergie entre les atomes ou molécules constituant le matériau qui sont proches les uns des autres. La chaleur se propage ainsi de proche en proche.
Convection
Lorsqu’on a affaire à un fluide, si celui-ci est immobile, le phénomène de conduction a lieu de manière similaire. Mais ce n’est généralement pas le cas et les mouvements du fluide étant généralement assez rapides par rapport aux échanges de chaleur. Lorsque le fluide est en contact avec une surface chaude par exemple, il emporte de l’énergie dans son mouvement ce qui accélère les échanges de chaleur.
Exemple: Lorsqu’on souffle sur un objet chaud pour le refroidir, on utilise la convection pour augmenter les échanges de chaleur
On distingue généralement deux types de convections:
- La convection forcée lorsque le mouvement du fluide est provoqué par une cause extérieure (par exemple un ventilateur)
- La convection naturelle lorsque le mouvement du fluide est provoqué par les différences de température.
Exemples de convections naturelles:
Un convecteur (on voit bien d’où vient son nom) électrique est un appreil de chauffage présentant une surface chaude et verticale . L’air qui se réchauffe à son contact voit sa densité diminuer, ce qui le fait se déplacer vers le haut. de l’air froid vient le remplacer ce qui entretient le mouvement. Faîtes l’expérience: Placez votre main au dessus d’un convecteur en fonctionnement vous sentirez nettement un courant d’air bien qu’il n’y ait aucun ventilateur.
A une plus grande échelle, ce sont des phénomènes de ce type qui sont responsable de l’existence des vents sur la planète terre.
Le Rayonnement:
Ce mode de transfert de chaleur n’a pas besoin du support de la matière et peut s’effectuer à travers le vide. En effet, il s’agit d’un transport d’énergie sous la forme d’ondes électromagnétiques. C’est à dire d’ondes de la même nature que la lumière.
Exemples:
La lumière et la chaleur du soleil nous parviennent à travers le vide sidéral
La chaleur qu’on ressent en nous approchant des braises laissées par un feu nous parvient sous la forme de rayonnement. L’air est transparent pour le rayonnement.
8.2 Conduction en régime permanent
Nous nous limiterons essentiellement à une dimension.
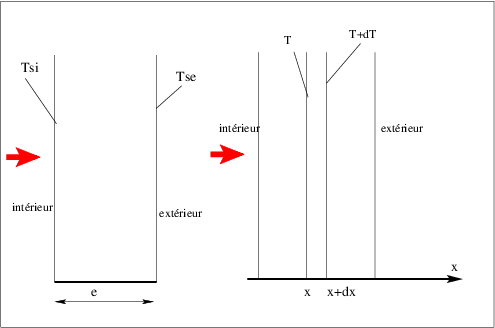
8.2.1 Conduction à travers une paroi plane en régime permanent.
Considérons une paroi plane constituée d’un matériau homogène et séparant deux milieux de températures différentes mais maintenues constantes dans le temps. Du fait de la différence de températures, un flux de chaleur va traverser cette paroi. L’expérience montre que ce flux est proportionnel à la surface et à la différence de températures entre les deux surfaces. De même, le flux est inversement proportionnel à l’épaisseur de la paroi ce qui donne une formule du type:
où S est la surface, e l’épaisseur et lambda un facteur de proportionnalité dont on donnera une interprêtation plus loin.
ou encore
après avoir défini le flux surfacique:
Loi de Fourier à une dimension:
En examinant ce qui se passe entre deux plans infiniments voisins dans la paroi (voir figure 8.1↓), on peut écrire:
ceci est la loi de Fourier pour le cas où la chaleur se propage dans une seule direction celle de l’axe ox.
Remarque: le signe - indique que la chaleur se déplace ves les températures décroissantes. (On compte le flux positivement dans le sens de la direction ox)
Remarque: Dans le cas où la chaleur se propage dans toutes les directions, la loi de Fourier s’écrit à l’aide des 3 dimensions d’espace (x,y,z) et doit faire intervenir des fonctions à plusieurs variables. La solution de tels problèmes est beaucoup plus complexe et on a aujourd’hui recours à des programmes informatiques pour réaliser les calculs numériquement. (ce cas ne sera pas traité ici)
La constante
apparaît comme une caractéristique du matériau indiquant avec quelle “vitesse” le matériau est traversé par la chaleur. On appelle ce paramètre la conductivité thermique. Les grandes valeurs de
correspondent à un matériau qui laisse passer la chaleur. On dit d’un tel matériau qu’il est conducteur. En revanche, une faible valeur de
correspond à un matériau ne laissant pas passer la chaleur facilement dont on dira alors qu’il est isolant.
Remarque: dans certains ouvrages,
est nommée conductibilité et est quelquefois notée par la lettre
.
Question: Quelle doit être l’unité de cette grandeur dans le système S.I.
Réponse: En exprimant
en fonction des autres grandeurs physiques:
on peut déduire l’unité de conductivité thermique soit:
Vous trouverez dans le tableau ci-dessous quelques exemples de valeurs de la conductivité pour différents matériaux conducteurs et isolants. Notez bien les ordres de grandeur.
| Matériau | conductivité en |
| conducteurs | |
| diamant | 550.0 |
| Argent pur | 417.1 |
| Cuivre pur | 386 |
| or pur | 297.7 |
| Aluminium pur | 229 |
| Duralumin | 164 |
| fer pur | 83.5 |
| isolants | |
| mousse de polyuréthane | 0.026 |
| Teflon (PTFE) | 0.24 |
| autres | |
| eau | 0.603 |
| glace | 2.2 |
| verre | 1.13 |
Remarque: Lorsqu’on doit traiter un problème de conduction thermique (ou d’isolation), le plus difficile est souvent de trouver des valeurs réalistes de la conductivité thermique. On pourra en trouver dans les ouvrages cités en référence ou encore dans certaines bases de données disponible sur Internet telles que:
-
http:// srdata.nist.gov/insulation/
Ce lien pointe sur une base de donnée du NIST (National Institute of standards and Technology) dédiée aux propriétés des isolants thermiques. -
http://www.apo.nmsu.edu/Telescopes/SDSS/eng.papers/
19950926_ConversionFactors/19950926_MProperties.html
Ce lien donne les valeurs de différentes propriétés pour un petit nombre de matériaux.
8.2.2 Régime permanent.
En régime permanent, le flux traversant chaque tranche de la paroi est le même. On a donc:
ce qui implique:
On a donc un profil de température linéaire comme sur la figure 8.2↓
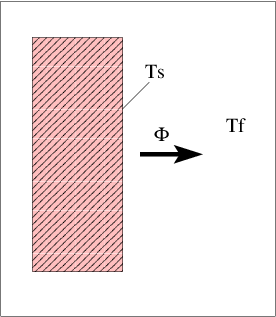
8.2.3 Interface avec un fluide: loi de Newton
Les températures utilisées ci- dessus sont celles du matériau et à la limite celles de sa surface. Mais que se passe-t-il à l’interface entre le matériau et le fluide avec lequel il est en contact. Généralement la température du fluide est différente de celle de la paroi et il y a donc un échange de chaleur. On considère généralement que le flux de chaleur entre la paroi et le fluide est proportionnel à la surface et à la différence de températures ce qui donne la
loi de Newton:
où
est appelé coefficient d’échange de chaleur par convection. Ce coefficient dépend généralement d’un grand nombre de paramètres caractérisant les conditions de l’échange comme par exemple la vitesse d’écoulement du fluide. L’essentiel des problèmes de convection consiste à évaluer ce coefficient.
- soit mesuré expérimentalement
- soit évalué grâce à une corrélation établie par des études antérieures (voir chapitre convection)
Le coefficient de convection sera donné dans la plupart des problèmes envisagés ici.
Note:
est la différence de température entre la surface du matériau et la masse du fluide (assez loin de la paroi pour que celle-ci n’ait pas d’influence sur le fluide). On ne précise pas le signe de
car tout dépend des conventions sur le flux.
Pour fixer les idées on peut par exemple décider de compter positivement le flux sortant du matériau on aura alors:
où
est la température de surface du matériau et
la température du fluide loin de la surface.
8.3 Notion de résistance thermique
8.3.1 Géométrie plane mur composite
Résistance de conduction
Considérons un mur composé de plusieurs couches de différents matériaux et de différentes épaisseurs. Si l’on est en régime permanent, le flux traversant les différentes couches est le même. (Sinon, la température devrait varier dans une couche ou le flux entrant est différent du flux sortant.
Prenons l’exemple de la figure 8.4↑. Le flux traversant la première couche s’écrira:
De même à travers la deuxième couche:
On peut alors remarquer que la différence de température totale s’écrit:
On appelle alors le terme
résistance thermique de conduction à travers la couche considérée.
On écrira alors en faisant abstraction du signe:
L’interprêtation de la formule précédente est la suivante: Les deux résistances thermiques représentent la résistance opposée par chaque couche au passage de la chaleur. Dans le cas présent, les deux résistances thermiques s’ajoutent pour former une résistance globale des deux couches au passage de la chaleur.
Il est quelquefois utile de définir une résistance thermique par unité de surface qu’on notera
.
On aura donc dans ce cas:
Résistance de convection
A la surface du mur on utilisera la loi de Newton pour calculer le flux:
De la même manière, on peut introduire une résistance thermique de convection définie par:
Revenons à la figure 8.4↑. On peut écrire:
soit
ici encore, la résistance thermique globale est la somme des résistances thermiques.
Résistance de contact
Il arrive que lorsque deux solides sont en contact, le contact ne soit pas parfait. On observe alors en régime permanent un saut de température entre les deux faces en contact. Ce saut de température peut être attribué à une résistance de contact
. On écrit alors:
où
est la différence de température entre les deux faces.
8.3.2 Géométrie cylindrique
Nous avons défini au paragraphe précédent une résistance thermique pour lae cas d’un mur plan. Lorsqu’on a affaire à un problème où la géométrie est cylindrique (ce qui est souvent le cas lorsqu’on a des tuyaux), l’expression des résistances thermiques sera différente.
Résistance de conduction
Considérons un tube tel que celui représenté sur la figure 8.5↑ . Pour calculer le flux de chaleur passant de l’intérieur du tube vers l’extérieur, on va revenir à la loi de Fourier. Le tube est représenté en coupe sur la figure 8.5↑ et on va considérer le flux passant entre deux surfaces cylindriques de rayons r et r+dr. Lorsqu’on est en régime permanent et pour les mêmes raisons que ci-dessus, le flux de chaleur entrant dans la masse du tuyau est le même que le flux sortant. On peut même ajouter que le flux sera le même à travers n’importe quelle surface cylindrique de rayon r dans la masse du tuyau. Le flux s’écrit:
où
est la longueur du tube. Le flux étant constant, on a là une équation différentielle très simple qui se résout aisément par intégration après avoir séparé les variables:
ce qui donne:
On en déduit immédiatement l’expression de la résistance thermique par conduction dans cette géomérie:
S’il y a plusieurs couches cylindriques, les résistances thermique s’additionneront comme dans le cas précédent.
note:
On peut aussi définir une résistance thermique par unité de longueur dont l’expression sera évidemment:
Résistance thermique de convection
Dans le cas du tube présenté sur la figure 8.5↑, il existe aussi une résistance de convection sur la face intérieure du tube de même qu’à la surface extérieure. De même que précédemment, la loi de Newton conduit immédiatement à
8.3.3 Géométrie sphérique
Ce cas pourra être traité à titre d’exercice de manière similaire.
8.3.4 Résistances en parallèle
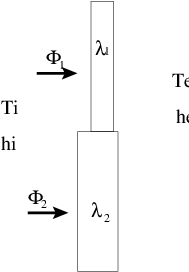
Imaginons une paroi constituée de deux pans différents constitués de deux matériaux différents et d’épaisseurs différentes comme indiqué sur la figure 8.6↑. Si l’on calcule séparément les deux flux traversant chacun des deux pans de paroi, on est amené à définir deux résistances thermiques distinctes:
Le Flux total passant à travers l’ensemble de la paroi peut alors s’écrire:
On peut alors définir une résistance thermique équivalente
telle que:
8.3.5 Coefficients de transferts globaux
Lorsqu’on traite le cas d’un bâtiment, on est quelquefois amené à définir un coefficient de transfert global
moyen pour la surface de murs. On peut alors écrire:
où
est la surface totale de mur séparant l’intérieur de l’extérieur et
la différence de température entre l’intérieur et l’extérieur.
On définit aussi quelquefois un coefficient par unité de volume
. On écrit alors
où
est le volume du bâtiment.
8.4 Analogie électrique
Une analogie est une correspondance entre deux phénomènes physiques distincts gouvernés par des lois semblables. Nous allons établir ici une analogie entre les phénomènes thermiques et électriques. Nous nous limiterons ici aux résistances thermiques de convection et de conduction en régime permanent. En réalité l’analogie peut être poussée plus loin. La correspondance est donnée dans le tableau ci-dessous:
| Thermique | électrique | ||
| Température | Potentiel électrique | ||
| Différence de température | Tension ou différence de potentiel | ||
| Flux de chaleur | Intensité du courant | ||
| Loi d’Ohm | |||
| Résistances en série | |||
| Résistances en parallèle |
Utilisation en pratique
En pratique pour utiliser cette analogie, on réalise un circuit électrique équivalent au problème thermique en disposant des résistances électriques dont les valeurs sont proportionnelles aux résistances thermiques. On impose ensuite une tension connue aux bornes du circuit correspondant aux points où la température est connue. Les courants s’établissant dans les différentes branches du circuit doivent alors être proportionnels aux flux de chaleur correspondants dans le problème thermique.
Par exemple, supposons qu’on construise un circuit électrique pour lequel les valeurs des résistances sont déterminées par
on prendra par exemple
.
Si l’on impose une tension telle que
(on prendra par exemple
), le flux de chaleur pourra être recalculé à partir des courants mesurés par: