1 Introduction
Notions de base: Température, énergie, propriétés des fluides
1.1 Objectifs de ce cours:
Il est utile, avant de commencer de préciser les objectifs poursuivis dans cet exposé: Ils seront de deux ordres: d’une part la connaissance scientifique , d’autre part les très nombreuses applications techniques.
du point de vue scientifique, les notions suivantes seront abordées
- L’énergie, sa conservation (premier principe)
- L’entropie, son caractère non conservatif (deuxième principe)
- Les propriétés des fluides ( gaz, liquides, vaporisation.....)
Les différents modes de transfert de chaleur
du point de vue des aplications, nous verrons notamment:
- les moteurs (différents cycles, turbines ...)
- les machines frigorifiques
- La climatisation
- l’isolation thermique.
L’étude des différentes machines thermiques s’appuiera sur le comportement thermodynamique des fluides. C’est pourquoi nous commencerons par comprendre ce comportement en relation avec la notion d’énergie.
1.2 Coup d’oeil historique.
La thermodynamique classique s’est essentiellement développée au 19ème siècle sous l’impulsion du développement du machinisme et en particulier de la machine à vapeur.
Parallèlement aux essais empiriques des “inventeurs” un certain nombre de tentatives de compréhension théorique des phénomènes ont lieu. Au début du siècle, on considère la chaleur comme un fluide qui s’écoule dans la matière et qui se conserve. Cette idée fausse sera dissipée au cours du siècle au fur et à mesure que les relations entre chaleur et travail mécanique seront précisées. Sadi Carnot qui est encore imprégné de cette idée, joue néammoins le rôle de précurseur et dans son essai de 1824 “Réflexions sur la puissance motrice du feu” pose déjà les bases de ce qu’on appellera plus tard le deuxième principe de la thermodynamique.
Viennent ensuite les travaux de Mayer, de Joule puis de Thomson et Clausius qui précisent les relations entre chaleur, température, travail. On doit notamment à Clausius la notion subtile d’entropie que nous aborderons dans le chapitre sur le deuxième principe. Vers la fin du siècle, la thermodynamique dite classique est bien établie avec ses deux principes et les notions d’énergie interne et d’entropie. C’est vers cette époque que l’américain W.J. Gibbs développe les applications de cette science à la chimie et en particulier aux mélanges fluides multiphasiques. Enfin, il manquait une interprêtation microscopique de la thermodynamique qui est réalisée par L. Boltzmann qui développe au début du 20ème siècle la thermodynamique statistique. En effet, à cette époque, la théorie atomique a complètement supplanté la théorie de la matière continue et la thermodynamique statistique pourra aussi être appliquée à des assemblées d’objets quantiques. Aujourd’hui, la thermodynamique joue un rôle dans un grand nombre d’applications qui vont de la biologie à la cosmologie en passant par la science des matériaux. Nous nous contenterons pour notre part d’introduire les concepts d’énergie et de voir les applications aux machines thermiques.
1.3 Propriétés de la matière:
Nous allons tout d’abord rappeler quelques faits établis sur la nature de la matière et préciser un certain nombre de notions sur lesquelles nous reviendrons constamment:
On peut observer la matière à différentes échelles. Elle nous apparaît alors sous des aspects bien différents.
- aspect microscopique: La matière est constituée d’innombrables particules qui sont en perpétuel mouvement. Par exemple, les gaz sont constitués d’atomes ou de molécules dont le mouvement est très libre du fait de la faible densité. Seuls quelques chocs (peu nombreux relativement au nombre de molécules) vont modifier les mouvements. Dans le cas d’un solide cristallin, l’agitation se traduit par des vibrations des atomes autour de leur position d’équilibre.
-
aspect macroscopique: Le résultat au niveau macroscopique de cette agitation microscopique est traduit par des grandeurs physiques que nous appellerons des paramètres macroscopiques.
- Température: C’est le paramètre qui traduit au niveau macroscopique l’énergie cinétique du système de particules en mouvement. En d’autres termes, plus les particules bougent, plus la température est élevée.
- Pression: Dans un fluide, les particules en mouvement s’entrechoquent ce qui induit des forces qui rapportées à la surface vont donner des pression. En particulier, les particules venant frapper la paroi du réservoir qui contient le fluide vont créer sur celle-ci une force dite de pression.
- Système thermodynamique: On appelle système thermodynamique une quantité de matière bien définie généralement séparée du milieu extérieur par une surface fermée appelée frontière. Étudier ce système du point de vue thermodynamique consiste à analyser ses échanges d’énergie avec le milieu extérieur et de relier ceux-ci à l’évolution de l’état de ce système.
- Etat d’équilibre thermique: C’est un état du système qui en l’absence d’échange d’énergie avec l’extérieur, ne doit pas changer. C’est à dire que si on isole le système du milieu extérieur en lui interdisant tout échange d’énergie avec le milieu extérieur, l’état du système restera inchangé. Ceci implique en particulier que le système doit être homogène en température. (Température égale en tout point du système)
On trouvera ci-dessous une description de certaines grandeurs caractérisant l’état du système:
1.3.1 Pression:
La pression est définie comme le rapport d’une force à une surface:
. La pression est une grandeur scalaire contrairement à la force qui est vectorielle. La pression dans un fluide est en effet indépendante de l’orientation de la surface sur laquelle s’exerce la force de pression. L’unité S.I. est le Pascal (Pa) qui est égal à 1N/m.
Les autres unités usuelles sont: le bar (bar) qui vaut
l’atmosphère (atm) qui vaut:
le Torr (Torr) correspond à la presion exercée par une colonne de mercure de 1mm de hauteur ce qui correspond environ à 133,3 Pa.
note:
Les unités données ci- dessus ont été nommées ainsi en hommage à la contribution des personnages suivants:
Blaise Pascal (1623-1662): Célèbre physicien et mathématicien Français inventeur notamment d’une des premières machines à calculer et auteur de recherches sur la transmission des pressions dans les liquides. Il a aussi écrit des essais philosophiques dont les fameuses“Pensées”.
Torricelli (1608- 1647) Mathématicien et physicien italien a collaboré avec Galilée vers la fin de la vie de celui-ci est l’inventeur du baromètre qui porte son nom et qui est constitué d’un tube de mercure renversé dans un récipient à l’air libre. La hauteur de la colonne de mercure indique la pression atmosphérique.
1.3.2 Température:
La température est une indication de l’agitation régnant au niveau microscopique. Elle est mesurée par un thermomètre qui est un dispositif physique dont une grandeur varie avec la température. Il existe une grande variété de types de thermomètres selon la grandeur physique prise comme témoin. Le premier et le plus connu a attribué à Galilée (vers 1640) utilise des ludions de différentes densités plongés dans un liquide. Les thermomètres à colonne de liquide (souvent du mercure) qui lui ont succédé ont dominé pendant longtemps mais sont en voie de disparition pour des raisons pratiques et écologiques. Les autres modèles font appel à la mesure d’une résistance electrique (sonde à résistance de platine) à des thermocouples, à des thermistances, à des capteurs à semiconducteurs.
La mesure de la température et la définition des échelles de températures est un sujet complexe que nous n’aborderons pas ici. Il nous suffira de savoir qu’il existe différentes échelles de températures et de connaître leurs correspondances.
Les échelles Celsius et Farenheit héritées du passé ont un zéro arbitraire tandis que l’échelle Kelvin est une échelle thermodynamique qui introduit le Zéro absolu. (Température en dessous de laquelle on ne peut pas descendre qui correspondrait à l’arrêt de tout mouvement microscopique)
-
L’échelle Celsius est une échelle affine posédant 2 points fixes:
- 0°C correspond à la température de fusion de la glace
- 100°C corrspond à la température d’ébullition de l’eau sous une pression de 1 atm.
-
L’échelle Farenheit encore en usage dans les pays anglo-saxons est basée sur des points fixes différents. la correspondace est la suivante:
- 0°C --> 32°F
- 100°C —> 212°F
- L’échelle Kelvin est une échelle thermodynamique vraie. Elle ne nécessite qu’un seul point fixe et coincide avec l’échelle des gaz parfaits. (voir plus loin). La correspondance avec l’échelle Celsius est la suivante: T(K) = t(°C) + 273,15. C’est à dire que la température de la glace fondante est de 273,15 K et celle de l’eau en ébullition sous 1 atm est de 373,15 K.
1.3.3 Représentation de l’état d’un système:
L’état d’un système est caractérisé par un certain nombre de paramètres physiques macroscopiques. Pour un fluide pur, dont la masse est fixée, l’état du système sera caractérisé par la pression, la température et le volume occupé par le gaz. En règle générale, ces trois paramètres sont liés par une relation appelée équation d’état en sorte que deux seulement sont indépendants (voir plus loin). La représentation la plus classique consiste à placer un point sur un diagramme dont l’abscisse est le volume et l’ordonnée la pression. Un tel diagramme est appelé diagramme de Clapeyron. On trace généralement sur un tel diagramme les courbes reliant tous les points représentant des états correspondant à une même température. De telles courbes son appelées courbes isothermes (voir figure ci dessous). Ces courbes sont analogues aux courbes de niveau qu’on trouve sur les cartes géographiques de randonnée, l’altitude étant l’analogue de la température.
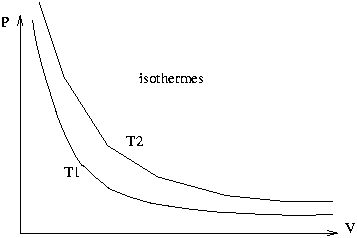
représentation de l’évolution d’un système dans un diagramme de Clapeyron.
- evolution réversible (première approche). Il s’agit ici d’une première approche, nous reviendrons longuement sur le sujet. L’évolution d’un système modifie généralement l’état du système. Si l’évolution est lente (par raport au temps de remise à l’équilibre), le système peut être considéré à chaque instant dans un état de quasi-équilibre. On est alors fondé de représenter l’évolution par une ligne continue sur le diagramme.
- evolution réelle (irréversible). Dans ce cas, on connaît généralement l’état initial et l’état final qui sont représentés par 2 points sur le diagramme. Pour représenter une telle évolution on relie les 2 points par une ligne en pointillés pour bien signifier que les états intermédiaires ne sont pas forcément atteints.

Rappels de notions de mécanique
1.3.4 L’énergie en mécanique
Dans toutes les transformations variées qui sont étudiées en physique, une grandeur joue un rôle fondamental: c’est l’énergie. Cette notion apparaît d’abord en mécanique où elle signifie: capacité de travail. Le travail est défini en mécanique comme une grandeur scalaire: produit scalaire de la force et du déplacement. Il est exprimé en joules (
avec
.
Le travail peut avoir le signe positif ou négatif. Positif si le déplacement est dans le sens de la force, nous disons qu’il y a travail moteur. Négatif si le déplacement se fait en sens contraire de la force, nous l’appelons alors travail résistant. Un système mécanique susceptible de fournir du travail contient de l’énergie.
Energie potentielle si cette énergie est due à la position des éléments du système dans l’espace.
- Ex: un lac de barrage rempli d’eau en montagne. L’énergie potentielle est par définition mesurée par le travail que l’eau peut fournir par sa chute jusqu’au niveau de référence. Si la hauteur de la chute est h et le poids de l’eau Mg, elle vaudra:

- Ex: énergie potentielle d’un gaz comprimé. En se détendant ce gaz peut fournir du travail, il peut actionner une turbine.
- Un corps en mouvement est susceptible de fournir du travail. Il possède de l’énergie cinétique.
- Ex: dans les moulins à vent ou les éoliennes nous utilisons l’énergie cinétique des masses d’air qui se déplacent pour produire du travail.
1.3.5 Conservation de l’énergie mécanique.
Une grande loi domine la mécanique, c’est la loi de conservation de l’énergie mécanique. Dans les phénomènes purement mécaniques (sans frottement, sans production ou dissipation de chaleur) l’énergie mécanique se conserve. C’est à dire: En l’absence d’efforts extérieurs, si un système perd de l’énergie potentielle il gagne de l’énergie cinétique et réciproquement.
1.3.6 Expression du travail des forces de pression
Nous aurons à évaluer fréquemment un travail mécanique exercé sur un fluide par le milieu extérieur.
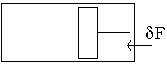
Soit un gaz enfermé dans un corps de pompe par un piston mobile.
A l’état d’équilibre les forces extérieures
exercées sur le gaz par le piston équilibrent les forces de pression que le gaz exerce sur la face intérieure du piston.
Si S représente la surface du piston et
la pression du gaz, cette force est égale à
.
Si le piston subit un déplacement dx vers la droite, le volume du gaz augmente de
et le gaz effectue contre le milieu extérieur le travail:
.
Pour un déplacement fini ce travail sera égal à:
somme à calculer entre le volume initial et le volume final du gaz.
Ce travail est calculable si la relation entre pression P et volume V est connue. Cette relation peut être représentée par une courbe:
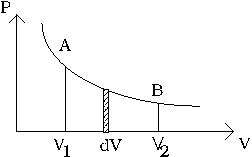
Le travail total
sera représenté par l’aire sous la courbe entre les points A et B.
En thermodynamique on s’intéresse plutôt au travail
exercé par les forces extérieures au sytsème. Lorsque le mouvement du piston est infiniment lent et que les énergies cinétiques sont négligeables, c’est à dire lorsque l’évolution est réversible (voir plus loin), le travail
effectué par les forces de pression du gaz contre le milieu extérieur est égal et de signe opposé au travail W effectué par les forces extérieures s’exerçant sur le gaz. Donc dans ce cas et uniquement dans ce cas:
1.3.7 Notions fondamentales en thermodynamique
Notion de température
Nous en avons déja parlé au paragraphe 1.3.2↑. Cette notion est différente de celle de quantité de chaleur. La distinction entre ces deux notions est due à Black, physicien britannique au XVIIIe siècle.
La température ’est un des paramètres caractérisant l’état d’un système. Sa valeur est reliée à l’agitation moléculaire. Elle a son origine dans nos sensations: un corps nous paraît, au toucher, froid, tiède ou chaud. Des changements dans l’état physique des corps accompagnent les modifications de ces sensations. Nous observons des changements d’état: l’eau de glace se transforme en liquide puis en vapeur quand la température augmente. Les métaux chauffés fondent. Nous observons également des variations continues des dimensions des corps qui s’échauffent, ce que nous nommons dilatation.
Le principe d’équilibre thermique énoncé ci-dessous permet de repérer les températures. On admet que les températures de deux corps en équilibre thermique sont égales.
* Deux corps mis en contact prolongé se mettent en équilibre thermique. C’est à dire qu’en l’absence d’intéraction avec le milieu extérieur, ils ne doivent plus évoluer.
* Deux corps mis en équilibre thermique avec un troisième sont aussi en équilibre thermique entre eux.
Grâce à ce principe un thermomètre permet de repérer non seulement sa propre température mais aussi celle du milieu dans lequel il est plongé. Ce qui fait son intérêt.
* Echelle Kelvin: c’est l’échelle de température absolue du système SI, elle est définie en prenant comme grandeur thermométrique le produit P.V d’un gaz parfait quelconque: L’échelle sera entièrement définie par le choix d’une température de référence. On choisit 273.16 pour la température du point triple de l’eau (état d’équilibre entre l’eau liquide, la glace et la vapeur d’eau). Il revient au même de poser:
avec
en Kelvin (K) et
en °C. Le zéro absolu est la température de 0 K, c’est la limite la plus basse des températures possibles. On ne peut jamais l’atteindre.
1.3.7.1 Notion de chaleur
La chaleur est une quantité d’énergie transférée entre deux systèmes matériels. Elle caractérise non pas un état du système mais une transformation du système, une modification de l’état du système. Le plus généralement (mais pas toujours), un échange de chaleur modifie la température du système. Un échange de chaleur est crée par une différence de température.
1.3.7.2 Notion de travail
Ce sera l’énergie échangée sous forme mécanique avec le milieu extérieur au cours d’une transformation. En thermodynamique, on s’intéresse au travail exercé par les forces extérieures au système. On considère le plus souvent le travail de déformation des fluides sous l’effet d’une pression extérieure. L’expression du travail élémentaire est dans ce cas, comme nous l’avons vu:
où
est la pression extérieure et
la variation de volume.
Le langage du thermodynamicien
- Système: corps ou ensemble de corps de masse déterminée et délimité dans l’espace. Le reste du monde est appelé \char‘ ̈milieu extérieur\char‘ ̈. Quand il n’échange pas de matière avec le milieu extérieur le système est dit fermé.
- Etat d’équilibre: un système est en état d’équilibre si, lorsqu’il est isolé du milieu extérieur, il ne se produit aucune modification à l’intérieur du système au cours du temps. Si ce n’est pas le cas il y a transformation du système.
- Transformation adiabatique: transformation sans échange de chaleur avec le milieu extérieur. Le système est thermiquement isolé du milieu extérieur. Elle est souvent utilisée comme modèle d’une évolution quasi instantanée.
- Transformation isotherme: transformation au cours de laquelle la température du système reste constante. Elle est souvent utilisée comme modèle d’une évolution infiniment lente.
- Transformation isochore: transformation au cours de laquelle le volume du système reste constant.
- Transformation isobare: transformation effectuée à pression constante. Elle est souvent utilisée pour les transformations ayant lieu à l’air libre (sous la pression atmospérique) exemple: réactions chimiques à l’air libre.
- Source de chaleur: c’est un milieu extérieur au système à température uniforme de capacité calorifique très grande par rapport à celle du système. Ainsi un échange de chaleur entre le système et la source de chaleur ne modifie pas la température de la source de chaleur. Quand un système est en contact avec une seule source de chaleur la transformation est dite monotherme.
- Cycle: lorsqu’un système initialement dans un certain état subit un certain nombre de transformations successives et lorsqu’à la fin de ces transformations il se retrouve dans un état d’équilibre final identique à l’état initial nous disons que le système a décrit un cycle.
1.4 Gaz parfait
1.4.1 Equation d’état et unités
Le gaz parfait est un gaz modèle, une approximation représentant le comportement thermoélastique des gaz aux basses pressions. Historiquement, il a éte introduit comme la limite des gaz réels pour des pressions tendant vers zéro. La loi des gaz parfaits, donnée ci après résume à elle seule les lois approchées mises en évidence au
siècle par les travaux de Mariotte, Charles, Gay-Lussac, Avogadro. Exemple: Loi de Mariotte: à température constante, le volume d’une masse donnée de gaz parfait varie en raison inverse de sa pression soit:
. L’isotherme d’un gaz parfait est donc représentée par une hyperbole dans un système d’axe (P,V). (Voir figure plus haut)
L’équation d’état d’un gaz parfait est:
avec: P pression en Pascals (Pa),
T température absolue Kelvin (K) n nombre de moles
R constante universelle des gaz parfaits (la même pour tous les gaz)
Avec les unités SI précisées ci-dessus, Rvaut:
Autres formes de l’équation d’état
A chaque gaz réel on associe un gaz parfait de même masse molaire M. ce qui donne:
où m est la masse et
Notons que la constante r est alors dépendante de la nature du gaz.
On trouve aussi parfois la loi des gaz parfaits exprimée en termes de volume molaire ou massique soit:
où
est le volume molaire
Applications
- Volume molaire normal d’un gaz parfait (Loi d’Avogadro)
C’est le volume d’une mole de gaz parfait à 0 °C, sous la pression d’une atmosphère. Il est indépendant de la nature du gaz et vaut:
- Masse volumique d’un gaz parfait
La masse volumique s’écrit, par définition:
Pour un gaz donné, elle est donc proportionnelle à sa pression et inversement proportionnelle à sa température absolue. Si
est la masse volumique dans les conditions
, la masse volumique
du même gaz dans les conditions
s’écrira:
Cette relation permet, par exemple, le calcul de la masse volumique dans des conditions quelconques à partir de la masse volumique normale.
- Densité d’un gaz par rapport à un autre
Par définition, la densité d’un gaz A par rapport à un gaz B est le quotient de la masse d’un volume du gaz A par la masse d’un volume égal du gaz B, les gaz étant pris dans les mêmes conditions de température et de pression.
C’est donc également le quotient de la masse volumique
de A par la masse volumique
de B.
La densité ne dépend pas des conditions de température et de pression; elle est égale au rapport des masses molaires. En particulier la densité par rapport à l’air (ou plus exactement au gaz parfait associé à l’air) est :
( où M est la masse molaire du gaz exprimée en grammes).
1.4.2 Mélanges de gaz parfaits
Lorsqu’on mélange deux gaz réels qui ne réagissent pas chimiquement l’un sur l’autre, le nombre de molécules du mélange est la somme des nombres de molécules des deux gaz. Il en est de même pour les gaz parfaits associés.
note: Le modèle du gaz parfait suppose que les molécules n’interagissent pas. Ce qui implique ici que chaque gaz se comporte comme s’il était seul à occuper le volume.
Pour simplifier, raisonnons sur deux gaz:
- pour le premier gaz:
- pour le deuxième gaz:
- pour le mélange:
est appelé pression partielle du gaz A (respectivement B) dans le mélange. Il s’agit de la pression que le gaz exercerait s’il était seul à occuper le volume. La pression totale P est alors la somme des pressions partielles.
Il est utile de caractériser la composition du mélange par les fractions molaires de chacun des gaz.
est la fraction molaire du gaz A dans le mélange.
Les propriétés suivantes sont faciles à démontrer :