Next: A propos de ce document ... Up: Epreuve de Technologie Thermique Previous: Etude de l'évaporateur d'une machine frigorifique

Correction

Dimensionnement de la surface:
1. Le flux peut être calculé du coté eau avec les données soit:
  
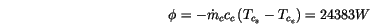
  $\begin{displaymath} \phi =-\dot{m}_{c}c_{c}\left( T_{c_{s}}-T_{c_{e}}\right) =24383W\end{displaymath}$
2. Il y a un changement d'état du côté fluide frigorigène ce qui mène à prendre un débit thermique infini car la température reste constante. On a donc:
  
  $\begin{displaymath} R=\frac{\left( \dot{m}_{c}c_{c}\right) }{\left( \dot{m}_{f}c_{f}\right) }=0\end{displaymath}$
  
  L'efficacité est définie comme le rapport $\frac{\phi }{\phi _{max}}$ soit:
  
  $\begin{displaymath} E=\frac{-\dot{m}_{c}c_{c}\left( T_{c_{s}}-T_{c_{e}}\right) }... ...{s}}}{T_{c_{e}}-T_{f}}=\frac{20-6}{20-\left( -10\right) }=0,467\end{displaymath}$
3. Pour $R=0$ , le NUT est toujours donné quelque soit la configuration par:
  
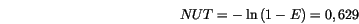
  $\begin{displaymath} NUT=-\ln \left( 1-E\right) =0,629\end{displaymath}$
4. De la définition du NUT, on tire:
  
  $\begin{displaymath} S=\frac{NUT\times \dot{m}_{c}c_{c}}{K}=0,730\end{displaymath}$
5. La surface d'échange dans un échangeur de ce type est la surface du tube intérieur soit 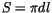$S=\pi dl$ d'où l'on tire:
  
  $\begin{displaymath} l=\frac{S}{\pi d}=11.6m\end{displaymath}$
Etude du fonctionnement après installation
Dans la nouvelle configuration, la surface reste la même puisque l'échangeur est déjà installé. On veut refroidir l'eau à la même température, seul son débit change. On peut aussi estimer que le coefficient d'échange n'a pas de raison de changer notablement.
1. Le NUT devient alors:
  
  $\begin{displaymath} NUT=\frac{KS}{\dot{m}_{c}c_{c}}=0,786\end{displaymath}$
2. La relation entre $E\textrm{ et }NUT$ est toujours la même. On en déduit:
  
  $\begin{displaymath} E=1-\exp \left( -NUT\right) =0,544\end{displaymath}$
3. Le nouveau flux se calcule immédiatement comme en 1a. seule la valeur du débit est différente:
  
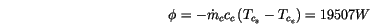
  $\begin{displaymath} \phi =-\dot{m}_{c}c_{c}\left( T_{c_{s}}-T_{c_{e}}\right) =19507W\end{displaymath}$
4. Le flux maximum est donné par:
  
  $\begin{displaymath} \phi _{max}=\dot{m}_{c}c_{c}\left( T_{c_{e}}-T_{f}\right) =\frac{\phi }{E}=35851W\end{displaymath}$
  
  Si l'on veut que la machine fonctionne dans ces conditions, il faut que la température d'évaporation change. On a:
  
  $\begin{displaymath} T_{f}=T_{c_{e}}-\frac{\phi _{max}}{\dot{m}_{c}c_{c}}=-5,73^{o}C\end{displaymath}$
Remarque: La donnée du débit de fluide frigorigène était inutile. Cela arrive aussi dans la vie. Certaines données, bien qu'accessibles, ne servent pas pour résoudre un problème précis que l'on se pose.