IUT de Saint Denis Module TMTHERM
CORRECTION G.I.M. 2
Contrôle de thermodynamique du Jeudi 23 janvier 2014
1 Machine frigorifique:
- La pression d’évaporation est donnée par la table de saturation du R143a. En effet, pour un corps pur, le changement d’état a lieu à pression et température constantes. La pression et la température sont liées par la courbe de pression de vapeur dont la table donne une représentation. A l’entrée de l’évaporateur, suite à la détente, on est en présence d’un équilibre liquide-vapeur. La température d’évaporation est de − 5°C, ce qui correspond à une pression d’évaporation de 5, 30 bar.
- Les hypothèses de l’énoncé indiquent que c’est un liquide saturé qui arrive à l’entrée du détendeur. La température de condensation sera donc de 35 °C. La pression correspondante est de 16, 23 bar.
- Il y a bien une surchauffe à la sortie de l’évaporateur. En effet, l’évaporation a lieu à − 5 °C tandis que la vapeur sortant de l’évaporateur est à 2°C et sous la pression de 16, 23 bar. La surchauffe est donc de 2 − ( − 5) = 7 °C. Lorsqu’il n’y a plus de liquide à évaporer, un apport de chaleur se traduit par une augmentation isobare de la température . C’est ce qui se passe à la fin, sur un petit bout de l’échangeur.
- L’enthalpie massique h1 du liquide arrivant au détendeur est donnée par la table de saturation. On sait qu’il s’agit de liquide saturé à la température de 35 °C , ce qui donne h1 = 254, 43 KJ ⁄ Kg.
- Le point 3 se trouve dans la zone surchauffée. On trouvera les caractéristiques de ce point sur la table de vapeur surchauffée sur l’isobare 5, 30 bar et à la température de 2°C, ce qui donne: h3 = 391, 27 KJ ⁄ Kg.
-
Lorsque la machine fonctionne à son point nominal, la puissance frigorifique produite est de Q̇f = 8, 2 KW. Il s’agit de la puissance absorbée par le fluide frigorigène dans son passage par l’évaporateur. Soit :\strikeout off\uuline off\uwave off Q̇f = ṁ(h3 − h2)\uuline default\uwave default d’après le premier principe appliqué à l’écoulement de fluide frigorigène dans l’évaporateur et compte tenu du fait que le travail utile est nul et que les variations d’énergie cinétique sont négligées. On en déduit:ṁ = (Q̇f)/(h3 − h2) = (8, 2)/(391, 27 − 254, 43) = 0, 0599 Kg ⁄ ssoit environ 60 g ⁄ s
-
Le titre de vapeur à l’entrée de l’évaporateur peut ^etre déduit de l’enthalpie massique h2 = h1 = 254, 43 KJ ⁄ Kg (la détente est isenthalpique). Il faut pour cela conna^itre les enthalpies massiques du liquide saturé et de la vapeur saturée à la température de − 5 °C . La table de saturation donne respectivement pour ces deux valeurs: h’ = h’( − 5 °C) = 192, 71KJ ⁄ Kg et h" = h"(35 °C) = 383, 68KJ ⁄ Kg . On en déduitx = (h2 − h’)/(h" − h’) = 0, 323
-
Le compresseur est adiabatiaque et on néglige les variations d’énergie cinétique. Le premier principe se réduit à :Ẇu = ṁ(h4 − h3) = 0, 0599.(424, 35 − 391, 27) = 1, 981 KWsoit environ 2 KW
- La compression n’est pas isentropique car l’entropie du point final s4 = 1, 7330 KJ ⁄ Kg.K est différente de celle du point initial s3 = 1, 7135 KJ ⁄ Kg.K. On peut également remarquer que s4 > s3, ce qui est bien conforme au deuxième principe.
2 Humidification d’air
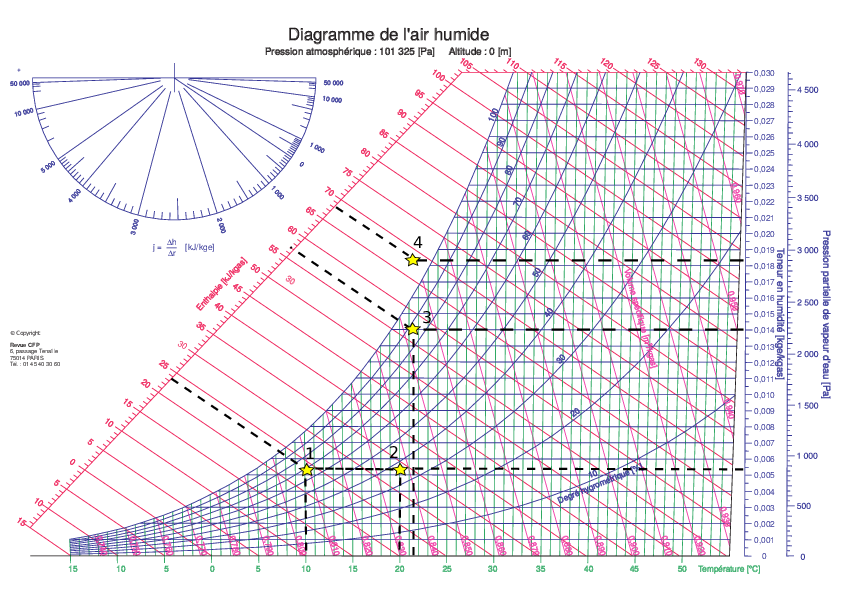
Dans une installation de traitement d’air, on aspire de l’air dans les conditions suivantes: Température T1 = 10 °C et humidité relative φ1 = 70% , débit d’air sec: ṁa = 0, 106 Kg ⁄ s. On considérera que la pression est constante et égale à 1 bar. Dans une première étape, cet air est chauffé par une série de résistances électriques jusqu’à une température de T2 = 20 °C . Par la suite, on injecte dans le flux d’air de la vapeur d’eau saturée à 100 °C . Le point final de cette dernière opération sera dénommé point 3. La mesure de l’humidité absolue de ce point donne: η3 = 0, 014 Kg ⁄ Kg a.s.
-
La pression de vapeur saturante de l’eau à 10 °C est donnée par la table de vapeur saturée soit: Ps1 = Ps(10 °C) = 0, 01227 bar. La pression partielle de la vapeur d’eau résulte de la définition de l’humidité relative :Pv1 = φ1.Ps1 = 0, 7*0, 01227 = 0, 008589 barl’humidité absolue quant à elle, peut être calculée à partir de la pression partielleη1 = (me)/(ma) = (Me)/(Ma) × (Pv)/(P − Pv) = 0, 622 × (0, 008589)/(1 − 0, 008589) = 0.00539 Kg ⁄ Kg a.ssoit environ 5, 4 g d’eau par Kg d’air sec.
-
L’air étant uniquement chauffé dans cette opération, il n’y a aucun apport d’humidité supplémentaire et l’évolution a lieu à pression constante. Par suite, ni l’humidité absolue, ni la pression partielle de la vapeur d’eau ne changent :η2 = η1 et Pv2 = Pv1
-
L’enthalpie de l’unité d’air humide est donnée par:h = h0 + cpa(T − T0) + η[cpv(T − T0) + Lv0]ce qui se réduit à:h1 = cpa t1 + η[cpv t1 + Lv0] = 5.64 Kcal ⁄ Kg = 23.61 KJ ⁄ Kg a.s.avec t1 = T1 − T0 = 10 °C . Les valeurs des chaleurs massiques de l’air et de l’eau son celles données dans le cours soit: cpa = 0, 24 Kcal.Kg − 1K − 1 et cpv = 0, 46 Kcal.Kg − 1K − 1 ainsi que celle de la chaleur latente de vaporisation de l’eau à 0 °C : Lv0 = 597 Kcal ⁄ Kg.
-
De même pour l’air après chauffage, h2 = cpa t2 + η[cpv t2 + Lv0] = 8, 06 Kcal ⁄ Kg = 33, 76 KJ ⁄ Kg a.s.
-
La puissance électrique consommée par les résistances est donné par l’application du premier principe à cet écoulement. Ici, il n’y a pas de travail utile ni de variation de l’énergie cinétique. Ce qui donne: Q̇ = ṁa(h2 − h1) = 0, 106(33, 76 − 23.61) = 1, 076 KW
-
L’enthalpie de l’unité d’air humide pour le flux d’air final dans l’état 3 est donnée par h3 = h2 + hv(η3 − η2) = 56, 79 KJ ⁄ Kg a.s.où hv est l’enthalpie massique de la vapeur injectée. Ici, il s’agit de vapeur d’eau saturée à la température de 100°C. celle-ci est donnée par la table de saturation de l’eau à savoir :hv = 639, 1 Kcal ⁄ Kg = 2674.6 KJ ⁄ Kg
note: On remarque que le point de référence de la table est bien cohérent avec celui qui est utilisé pour les calculs de l’enthalpie d’air humide, à savoir :h’ = 0 à 0 °C pour le liquide saturé. -
En inversant la formule donnant l’enthalpie de l’air humide (voir questions 3 et 4), on obtient :T3 = (h3 − η3Lv0)/(cpa + η3cpv) = (56, 79 − 0, 014 × 597 × 4, 185)/((0, 24 + 0, 014 × 0, 46)4, 185) = 21.15 °Cen ayant pris soin d’exprimer toutes les grandeurs énergétiques en KJ.
-
La pression partielle de la vapeur dans l’état final peut être calculée à partir de l’humidité absolue en inversant la formule utilisée questions 1 et 2.Pv3 = (η3P)/(0, 622 + η3) = 0.02201 bar
-
Le débit d’eau injecté dans le flux d’air au cours de la deuxième étape est donné par la différence entre le débit d’eau contenu dans le flux d’air sortant 3 et le débit d’eau contenu dans le flux d’air préchauffé arrivant en 2 soit : Δṁe = ṁe3 − ṁe2Δṁe = ṁe3 − ṁe2 = η3ṁa − η2ṁa = ṁa(η3 − η2) = 0, 0009128 Kg ⁄ ssoit environ 0, 91 g ⁄ s ou encore:3, 286 Kg ⁄ heure
-
On multiplie le débit d’eau injectée par un facteur 1,5. Connaissant ce nouveau débit injecté on peut en déduire l’humidité absolue η4 du nouveau point final de l’opération. On obtient η4 = (Δṁe)/(ṁa) + η2 = 0.0183on peut alors calculer l’enthalpie correspondante comme à la question 6 :h4 = h2 + hv(η4 − η2) = 68.31 KJ ⁄ Kg a.s.Le point correspondant sur le diagramme doit être en alignement avec les points 2et 3 dans le prolongement du segment 2 − 3. On constate que le point 4 est dans la zone de brouillard.