1 Gaz parfait

1. L’application de la loi des gaz parfaits donne: $$n=\frac{P.V}{R.T}=\frac{10^{5}.10.10^{-3}}{8,314\,.\,293,15}=\boxed{0,410\, mol}$$ soit une masse de $$m=n.M=\boxed{11,49\, g}$$
2. L’évolution du gaz se fait à volume constant, on peut écrire: ${\displaystyle \frac{P}{T}=cte}$ , soit: $$\frac{P_{2}}{T_{2}}=\frac{P_{1}}{T_{1}}\,\,\Rightarrow\,\, P_{2}=P_{1}\frac{T_{2}}{T_{1}}=10^{5}\frac{323,15}{293,15}=\boxed{1,102\,10^{5}\, P_{a}}$$
3. Le travail est nul car le volume ne varie pas. La quantité de chaleur reçue est égale à la variation d’énergie interne soit: $$Q=\Delta U=nC_{v}\left(T_{2}-T_{1}\right)=\boxed{255,84\, J}$$

2 Détente dans une turbine à gaz

1. L’évolution est adiabatique réversible, on peut utiliser la formule de Laplace ou son équivalent en variables (P,T) soit: $$P^{1-\gamma}T^{\gamma}=cte\,\,\,\,\, soit:\,\quad P_{2}^{1-\gamma}T_{2}^{\gamma}=P_{1}^{1-\gamma}T_{1}^{\gamma}$$ d’où l’on tire: $$T_{2}=T_{1}\left(\frac{P_{1}}{P_{2}}\right)^{\frac{1-\gamma}{\gamma}}=1073,15.12^{\frac{-0,3}{1,3}}=\boxed{604,8\, K}$$
2. Au cours d’une évolution adiabatique et réversible, la variation d’entropie est nulle. En effet lorsque l’évolution est réversible, l’inégalité exprimant le deuxième principe se réduit à une égalité. On a donc: $$\Delta S=\int\frac{\delta Q}{T}\,\,\,\, et\, puisque\,\,\delta Q=0\,\,\, finalement:\,\,\boxed{\Delta S=0}$$
3. Pour un gaz parfait, la variation d’enthalpie est donnée par ${\displaystyle \Delta H=mc_{p}\Delta T}$ . La variation d’enthalpie massique sera donc égale à : $$\Delta h=c_{p}\Delta T=1126\left(604,8-1073,15\right)=\boxed{-527,3\,10^{3}\, J}$$ on remarque que cette quantité est négative conformément à notre convention de signe. Ici, le gaz perd de l’énergie.
4. L’application du premier principe à l’écoulement dans la turbine donne:${\displaystyle \dot{W}=\dot{m}w=\dot{m}\Delta H=\dot{m}c_{p}\Delta T}$ dont on peut déduire: $$\dot{m}=\frac{\dot{W}}{\Delta h}=\frac{\dot{W}}{c_{p}\Delta T}=\frac{-2000\,10^{3}}{-527,3\,10^{3}}=\boxed{0,379\, kg/s}$$

3 Mélange de gaz parfaits

1. Calculer les fractions molaires des deux gaz dans ce mélange.
2. Calculer les nombres de moles d’azote et de vapeur d’eau ainsi que les masses correspondantes.
3. Par suite d’un refroidissement, la température baisse jusqu’à 20°C. Une partie de la vapeur d’eau est condensée (transformée en liquide) pour des raisons qui sortent du cadre de cet exercice (nous verrons cela au $3^{ème}$ semestre). On négligera le volume occupé par le liquide. La pression partielle de la vapeur d’eau dans le mélange s’établit alors à 0.0234 bar. On considère que le mélange resté sous forme gazeuse se comporte toujours comme un mélange de gaz parfaits. Calculer le nombre de moles d’eau restées à l’état de vapeur ainsi que la masse correspondante.
4. Calculer la pression partielle de l’azote ainsi que la pression totale dans cette nouvelle situation.
5. Calculer les fractions molaires des deux gaz dans cette nouvelle situation.
6. Justifier l’hypothèse selon laquelle le volume de liquide est négligeable.

• Masses molaires des gaz:   $M_{H_{2}O}=18\, g.mol^{-1}$    \strikeout off\uuline off\uwave off$M_{N_{2}}=28\, g.mol^{-1}$
• Constante universelle des gaz parfaits: $R=8,314\,\, J.mol^{-1}K^{-1}$
• Masse volumique de l’eau liquide à température ambiante: $\rho=10^{3}kg.m^{-3}$

4 Cycle de Joule

Figure 1 Cycle de Joule

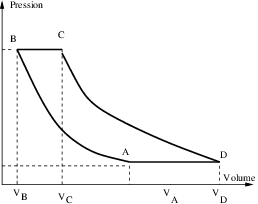
On considère une machine fonctionnant selon le cycle de Joule représenté par la figure 1↑. On considèrera que le fluide moteur est un gaz parfait dont on connait les chaleurs molaires $C_{p}$ et $C_{v}$ . Le rapport de ces chaleurs molaires sera noté $\gamma=\frac{C_{P}}{C_{v}}$ .

• Les évolutions AB et CD sont considérées comme adiabatiques et réversibles.
• Les évolutions BC et DA sont des isobares réversibles.
• On note $P_{1}=P_{A}=P_{D}$ ainsi que $P_{2}=P_{B}=P_{C}$ et on définit le rapport de compression $a=\frac{P_{2}}{P_{1}}$
• On réalisera l’analyse du cycle pour $n=$ 1 mole de gaz.

1. Exprimez $T_{B}$ en fonction de $T_{A}$ et des autres caractéristiques de la machine et du gaz. De même, exprimez $T_{C}$ en fonction de $T_{D}$ et des autres caractéristiques du problème.
2. Exprimez Les quantités de chaleur échangées par le fluide moteur au cours des évolutions BC et DA soit: $Q_{BC}$ et $Q_{DA}$ en fonction des températures.
3. Exprimez le rendement du moteur en fonction des deux quantités de chaleur déterminées ci- dessus et en déduire que le rendement peut s’écrire: $$\rho=1-a^{\frac{\gamma-1}{\gamma}}$$